特征工程
2.1 特征提取
将原始数据转化为实向量之后,为了 让模型更好地学习规律,对特征做进一步的变换。首先,要理解业务数据和业务逻辑。 其次,要理解模型和算法,清楚模型需要什么样的输入才能有精确的结果。
2.1.1 探索性数据分析
Exploratory Data Analysis (EDA)
在尽量少的先验假设条件下,探索数据内部结构和规律。是一种方法论而不是特点技术。
可视化
箱型图、直方图、多变量图、散点图…
定量技术
样本均值、方差、分位数、峰度、偏度。
2.1.2 数值特征
截断
太多的精度有可能是噪声。长尾数据可以先进行对数转换,然后截断。
二值化
标识是否存在。
分桶
如果跨越不同的数量级,则不是一个好特征。对于逻辑回归模型,一个特征对应一个系数,模型会对较大特征值敏感。
平均分桶
固定宽度的分桶。
幂分桶
根据10的幂来分桶,和对数变换相关。
分位数分桶
数值变量的取值存在很大间隔时候采用。
缩放
标准化缩放
将数值变量均值变为0,方差变为1。对目标变量为输入特征的光滑函数的模型,如线性回归和逻辑回归比较有效。
$x’ = \frac{x - avg(x)}{\sigma}$
健壮缩放
标准化缩放变种,采用中位数而非均值,对于有异常点的数据有用。
$x’ = \frac{x - median(x)}{IQR(x)}$
均值归一化
将数值范围缩放到 [-1, 1] 区间里,且数据的均值变为0。
$x’ = \frac{x - avg(x)}{max(x) - min(x)}$
最大最小值缩放
将数值范围缩放到 [0, 1] 区间里。
$x’ = \frac{x - min(x)}{max(x) - min(x)}$
最大绝对值缩放
This estimator scales and translates each feature individually such that the maximal absolute value of each feature in the training set will be 1.0. It does not shift/center the data, and thus does not destroy any sparsity.将数值范围缩放到 [-1, 1] 区间里。
$x’ = \frac{x}{|max(x)|}$
范数归一化
将数值变量某一范数变为1。
平方根缩放或对数缩放
对数缩放可处理长尾分且取值为正数的特征。
平方根缩放是方差稳定的变换。
缺失值处理
补值:均值,中位数,预测缺失值
忽略:将缺失作为一种信息进行编码直接喂给模型
特征交叉
数值特征之间的相互作用。对多个变量进行加减乘除等操作,在线性模型中引入非线性性质,提升模型表达能力。
非线性编码
线性模型很难学到非线性关系,采用非线性编码提升模型效果。
多项式核,高斯核
基因算法、局部特性嵌入、t-SNE等等。
行统计量
空值的个数,0的个数,正负值的个数等等。
2.1.3 类别特征
也叫做定性数据。没有数学意义。
自然数编码 label encoding
每一个类别分配一个编号。对类别编号进行洗牌,训练多个模型进行融合。
独热编码 one-hot encoding
每一个特征取值对应一维特征,得到稀疏的特征矩阵。
分层编码
取不同位数进行分层。可用于邮政编码、身份证号等有规律的特征。
散列编码 hash encoding
进行独热编码之前可以先对类别进行散列编码,避免矩阵过于系数。但是可能会导致特征取值冲突,影响模型效果。
计数编码 count encoding
将类别特征用对应的计数来代替。(就是根据每一个类别特征的类别对二分类标签进行sum求和得到每个类别中样本标签为1的总数)。对异常值敏感。特征取值可能冲突。
计数排名编码
将类别特征用对应的计数排名来代替。对异常值不敏感。特征取值不会冲突。
目标编码 target encoding
基于目标变量对类别特征进行编码。
对于C分类问题,目标编码后只需要增加C−1个属性列,如果C远远小于特征类别数量,则相对one-hot-encoding可以节省很多内存。用概率$P(y=y_i|x=x_i)$代替属性值x。
$f(y_j,x_i) = \lambda(n_i)P(y=y_j|x=x_i) + (1 - \lambda(n_i))P(y = y_j)$
$n_i$是训练集中$x_i$的样本个数。$\lambda(n_i)$用于计算概率值的可靠性(有可能特征包含$x_i$的样本数量比较小),取值范围是[0,1]。
2.1.4 时间特征
可提取信息:季度(初/末)、闰年、周末、节假日、营业时间。
滞后特征 lag
将时间序列预测问题转化为监督学习问题的一种经典方法。
滑动窗口统计特征
计算前n个值的均值。上面的滞后特征是一个特例,对应时间窗口宽度是1。另一种特殊的窗口设置包含所有历史数据,称为扩展窗口统计。
2.1.5 空间特征
可提取信息:经纬度、行政区ID、城市、两个位置之间的距离。
2.1.6 文本特征
自然语言处理,有字符转化小写等手段。
语料构建
构建一个由文档或者短语组成的矩阵,每一行是一个文档,每一列是单词。
文本清洗
剔除爬虫抓取文本的HTML标记。剔除停止词。统一编码。取出标点符号、数字、空格。还原为词根。
分词
词性标注
名词动词形容词。
词形还原和词干提取
抽取词的词干和词根形式。
文本统计特征
不需要考虑词序信息。文本长度、单词个数、特殊字符占比等等。
N-Gram模型
将文本转换成连续序列,包含那个元素。
Skip-Gram模型
词级模型
向量的每个分量取值0或1,代表是否在文档中出现。
词袋模型
向量的每个分量取值词语出现次数,为了减小维度,可以过滤掉词频太小的单词。
TF-IDF
Term Frequency词频:单词的重要性随其在文中出现次数的增加而上升。
Inverse Document Frequency逆文档频率:单词的重要性随其在语料库出现频率的增加而下降。
TF-IDF模型是经典的向量空间模型(Vector Space Model)。
余弦相似度
计算检索词之间的相关性。
Jaccard相似度
两个文档中相交的单词个数除以出现单词的总合
$J(d_1,d_2) = \frac{d_1 \bigcap d_2}{d_1 \bigcup d_2}$
编辑距离
Levenshtein。两个字符串由一个转成另外一个所需要的最少操作次数。
隐形语义分析
把高维向量空间模型表示的文档映射到低维的潜在语义空间。可以使用SVD。
Word2Vec
最常用的单词嵌入,包含单词的语义信息(分布式表示)。单词所在空间映射到低维的向量空间,每一个词对应一个向量,通过计算向量之间的余弦相似度可以得到单词间相似度。
2.2 特征选择
从原始数据的特征集合中选出一个子集。
目的:
- 简化模型,便于理解
- 改善性能
- 降低过拟合风险
前提:训练数据中包含冗余或者无关特征,移除之后不会导致信息丢失。
冗余:和无用有区别。一个特征本身有用,但与另外一个有用的特征强相关,则这个特征可能就是冗余的。
2.2.1 过滤方法 Filter
单变量过滤
不需要考虑特征之间的相互关系,基于特征变量和目标变量之间的相关性和互信息。
按照相关性对特征进行排序,过滤掉最不相关的特征。
优点
- 计算效率高
- 不易过拟合
- 可扩展
缺点
- 忽略特征之间的关系
- 忽略特征和模型之间的关系
举例
卡方检验,信息增益,相关系数
Pearson积差相关系数
用于量度两个变量X和Y之间的线性相关。 两个变量分别服从正态分布,通常用t检验检查相关系数的显著性;两个变量的标准差不为0。取值是[-1, +1],其中1是总正线性相关性,0是非线性相关性,并且-1是总负线性相关性。
$\rho_{X,Y} = {\mathrm {cov} (X,Y) \over \sigma _{X}\sigma _{Y}}={E[(X-\mu _{X})(Y-\mu _{Y})] \over \sigma _{X}\sigma _{Y}} = \frac{∑_1^n(X_i−\bar{X})(Y_i−\bar{Y})} {\sqrt{∑_1^n(Xi−\bar{X})^2∑_1^n(Yi−\bar{Y})^2}}$
Spearman秩相关系数
利用两变量的秩次大小作线性相关分析,对原始变量的分布不做要求,属于非参数统计方法。因此它的适用范围比Pearson相关系数要广的多。斯皮尔曼等级相关系数同时也被认为是经过排行的两个随机变量的皮尔逊相关系数,以下实际是计算x、y的皮尔逊相关系数。

Kendall秩相关系数
是一种秩相关系数,用于反映分类变量相关性的指标,适用于两个变量均为有序分类的情况。
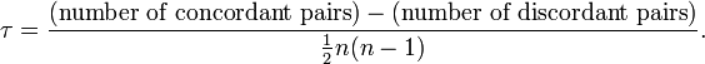
多变量过滤
优点
- 考虑特征之间的关系
- 计算复杂度适中
缺点
- 忽略特征和模型之间的关系
举例
CFS, MBF, FCBF
覆盖率
计算每个特征在训练集中出现比例。覆盖率太小的特征可以剔除。
皮尔森相关系数
度量两个变量之间的线性相关性。
$P_{X,Y} = \frac{cov(X,Y)}{\sigma_X\sigma_Y} = \frac{E[(X-\mu_X)(Y-\mu_Y)]}{\sigma_X\sigma_Y}$
Fisher得分
好的特征在同一个类别中取值相似,不同类别之间取值差异较大。
假设检验
假设特征和目标之间相互独立,作为H0假设。根据统计量确定p值。
互信息
互信息越大,两个变量相关性越高。
最小冗余最大相关性 Minimum Redundancy Maximum Relevance
mRMR使用多种相关性的度量指标。是一种贪心策略,某个特征一旦被选择,在之后不会删除。
相关特征选择 Correlation Feature Selection
CFS假设好的特征集合跟目标变量非常相关,但特征之间彼此不想关。
2.2.2 封装方法 Wrapper
过滤方法与具体的机器学习算法相互独立,因此过滤方法没有考虑选择的特征集合在具体机器学习算法上的效果。封装方法直接使用机器学习算法评估特征子集的效果。可以检测两个或多个特征之间的交互关系。
优点
- 让模型效果达到最优
- 有可能会卡在局部最优
缺点
- 计算量大
- 样本不够充分的情况下容易过拟合
举例
序列向前SFS,序列向后SBE,增q删r,随机爬山,基因算法
完全搜索
有穷举和非穷举。分支定界搜索配合剪枝比较实用。其他还有定向搜索,先选择N个得分最高的特征作为子集,将其加入一个限制最大长度的优先队列,每次从队列中取出得分最高的子集,然后穷举向该子集加入一个特征后产生所有特征集,将这些特征集加入队列。最优优先搜索在定向搜索的基础上,不限制队列长度。
启发式搜索
序列向前/后选择。双向搜索同时使用向前向后选择,在两者搜索到相同子集的时候停止。
随机搜索
执行序列向前/后选择,算法随机选择特征子集。
2.2.3 嵌入方法 Embedded
优点
- 计算效率高
- 考虑了机器学习算法的特点
缺点
- 依赖机器学习模型
举例
决策树,随机森林,梯度提升树,SVM,LASSO




